Convex Optimization

Convex Functions

We begin with a definition of the graph of a real-valued function.

Definition

The graph of $f: \Omega \rightarrow \mathbb{R}, \Omega \subset \mathbb{R}^n$, is the set of points in $\Omega \times \mathbb{R} \subset \mathbb{R}^{n+1}$ given by

$$\left\{\left[\begin{array}{c} \boldsymbol{x} \\ f(\boldsymbol{x}) \end{array}\right]: \boldsymbol{x} \in \Omega\right\} .$$

We can visualize the graph of $f$ as simply the set of points on a "plot" of $f(\boldsymbol{x})$ versus $\boldsymbol{x}$.

Definition

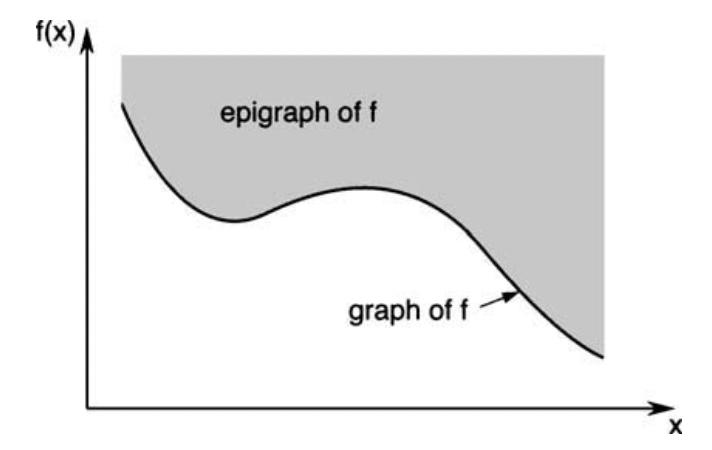
The epigraph of a function $f: \Omega \rightarrow \mathbb{R}, \Omega \subset \mathbb{R}^n$, denoted epi $(f)$, is the set of points in $\Omega \times \mathbb{R}$ given by

$$\operatorname{epi}(f)=\left\{\left[\begin{array}{l} \boldsymbol{x} \\ \beta \end{array}\right]: \boldsymbol{x} \in \Omega, \beta \in \mathbb{R}, \beta \geq f(\boldsymbol{x})\right\} .$$

The epigraph epi $(f)$ of a function $f$ is simply the set of points in $\Omega \times \mathbb{R}$ on or above the graph of $f$. We can also think of epi $(f)$ as a subset of $\mathbb{R}^{n+1}$.

Recall that a set $\Omega \subset \mathbb{R}^n$ is convex if for every $\boldsymbol{x}_1, \boldsymbol{x}_2 \in \Omega$ and $\alpha \in(0,1)$, $\alpha \boldsymbol{x}_1+(1-\alpha) \boldsymbol{x}_2 \in \Omega$. We now introduce the notion of a convex function.

Definition

A function $f: \Omega \rightarrow \mathbb{R}, \Omega \subset \mathbb{R}^n$, is convex on $\Omega$ if its epigraph is a convex set.

Theorem

If a function $f: \Omega \rightarrow \mathbb{R}, \Omega \subset \mathbb{R}^n$, is convex on $\Omega$, then $\Omega$ is a convex set.

Proof

We prove this theorem by contraposition. Suppose that $\Omega$ is not a convex set. Then, there exist two points $\boldsymbol{y}_1$ and $\boldsymbol{y}_2$ such that for some $\alpha \in$ $(0,1)$

$$\boldsymbol{z}=\alpha \boldsymbol{y}_1+(1-\alpha) \boldsymbol{y}_2 \notin \Omega .$$

Let

$$\beta_1=f\left(\boldsymbol{y}_1\right), \quad \beta_2=f\left(\boldsymbol{y}_2\right) .$$

Then, the pairs

$$\left[\begin{array}{l} \boldsymbol{y}_1 \\ \beta_1 \end{array}\right], \quad\left[\begin{array}{l} \boldsymbol{y}_2 \\ \beta_2 \end{array}\right]$$

belong to the graph of $f$, and hence also the epigraph of $f$. Let

$$\boldsymbol{w}=\alpha\left[\begin{array}{l} \boldsymbol{y}_1 \\ \beta_1 \end{array}\right]+(1-\alpha)\left[\begin{array}{l} \boldsymbol{y}_2 \\ \beta_2 \end{array}\right]$$

We have

$$\boldsymbol{w}=\left[\begin{array}{c} \boldsymbol{z} \\ \alpha \beta_1+(1-\alpha) \beta_2 \end{array}\right]$$

But note that $\boldsymbol{w} \notin$ epi $(f)$, because $\boldsymbol{z} \notin \Omega$. Therefore, epi $(f)$ is not convex, and hence $f$ is not a convex function.

The next theorem gives a very useful characterization of convex functions. This characterization is often used as a definition for a convex function.

Theorem

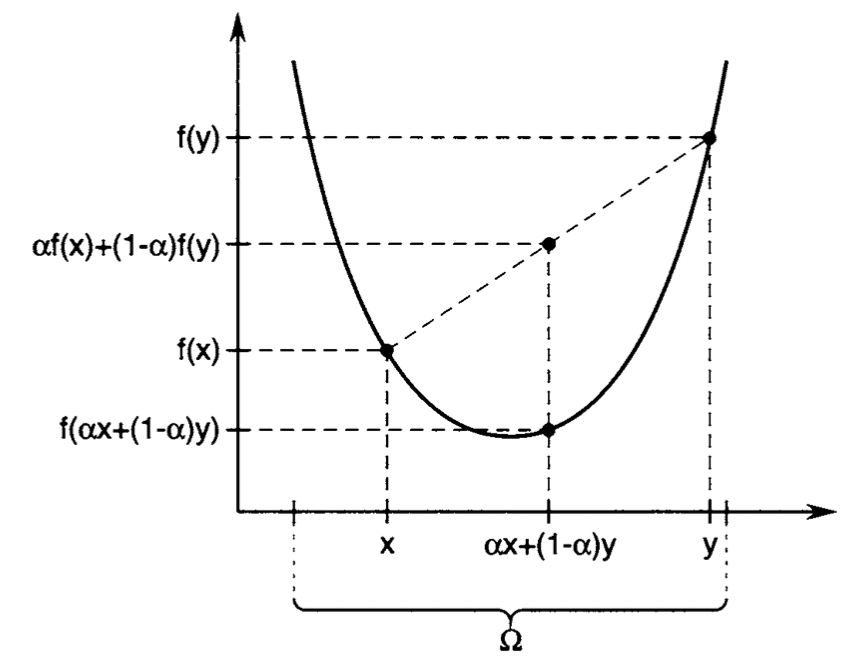
A function $f: \Omega \rightarrow \mathbb{R}$ defined on a convex set $\Omega \subset \mathbb{R}^n$ is convex if and only if for all $\boldsymbol{x}, \boldsymbol{y} \in \Omega$ and all $\alpha \in(0,1)$, we have

$$f(\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y}) \leq \alpha f(\boldsymbol{x})+(1-\alpha) f(\boldsymbol{y})$$

Proof

$\Leftarrow$ : Assume that for all $\boldsymbol{x}, \boldsymbol{y} \in \Omega$ and $\alpha \in(0,1)$

$$f(\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y}) \leq \alpha f(\boldsymbol{x})+(1-\alpha) f(\boldsymbol{y}) .$$

Let $\left[\boldsymbol{x}^{\top}, a\right]^{\top}$ and $\left[\boldsymbol{y}^{\top}, b\right]^{\top}$ be two points in epi $(f)$, where $a, b \in \mathbb{R}$. From the definition of epi $(f)$ it follows that

$$f(\boldsymbol{x}) \leq a, \quad f(\boldsymbol{y}) \leq b$$

Therefore, using the first inequality above, we have

$$f(\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y}) \leq \alpha a+(1-\alpha) b .$$

Because $\Omega$ is convex, $\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y} \in \Omega$. Hence,

$$\left[\begin{array}{c} \alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y} \\ \alpha a+(1-\alpha) b \end{array}\right] \in \operatorname{epi}(f)$$

which implies that epi $(f)$ is a convex set, and hence $f$ is a convex function. $\Rightarrow$ : Assume that $f: \Omega \rightarrow \mathbb{R}$ is a convex function. Let $\boldsymbol{x}, \boldsymbol{y} \in \Omega$ and

$$f(\boldsymbol{x})=a, \quad f(\boldsymbol{y})=b .$$

Thus,

$$\left[\begin{array}{l} \boldsymbol{x} \\ a \end{array}\right],\left[\begin{array}{l} \boldsymbol{y} \\ b \end{array}\right] \in \operatorname{epi}(f)$$

Because $f$ is a convex function, its epigraph is a convex subset of $\mathbb{R}^{n+1}$. Therefore, for all $\alpha \in(0,1)$, we have

$$\alpha\left[\begin{array}{l} \boldsymbol{x} \\ a \end{array}\right]+(1-\alpha)\left[\begin{array}{l} \boldsymbol{y} \\ b \end{array}\right]=\left[\begin{array}{c} \alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y} \\ \alpha a+(1-\alpha) b \end{array}\right] \in \operatorname{epi}(f)$$

The above implies that for all $\alpha \in(0,1)$,

$$f(\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y}) \leq \alpha a+(1-\alpha) b=\alpha f(\boldsymbol{x})+(1-\alpha) f(\boldsymbol{y})$$

This completes the proof. A geometric interpretation of the theorem is given below. The theorem states that if $f: \Omega \rightarrow \mathbb{R}$ is a convex function over a convex set $\Omega$, then for all $\boldsymbol{x}, \boldsymbol{y} \in \Omega$, the points on the line segment in $\mathbb{R}^{n+1}$ connecting $\left[\boldsymbol{x}^{\top}, f(\boldsymbol{x})\right]^{\top}$ and $\left[\boldsymbol{y}^{\top}, f(\boldsymbol{y})\right]^{\top}$ must lie on or above the graph of $f$.

Using the above theorem, it is straightforward to show that any nonnegative scaling of a convex function is convex, and that the sum of convex functions is convex.

Theorem

Suppose that $f, f_1$, and $f_2$ are convex functions. Then, for any $a \geq 0$, the function af is convex. Moreover, $f_1+f_2$ is convex.

Proof

Let $\boldsymbol{x}, \boldsymbol{y} \in \Omega$ and $\alpha \in(0,1)$. Fix $a \geq 0$. For convenience, write $\bar{f}=a f$. We have

$$\begin{aligned} \bar{f}(\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y}) & =a f(\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y}) \\ & \leq a(\alpha f(\boldsymbol{x})+(1-\alpha) f(\boldsymbol{y})) \text { because } f \text { is convex and } a \geq 0 \\ & =\alpha(a f(\boldsymbol{x}))+(1-\alpha)(a f(\boldsymbol{y})) \\ & =\alpha \bar{f}(\boldsymbol{x})+(1-\alpha) \bar{f}(\boldsymbol{y}) \end{aligned}$$

which implies that $\bar{f}$ is convex. Next, write $f_3=f_1+f_2$. We have

$$\begin{aligned} f_3(\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y})= & f_1(\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y})+f_2(\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y}) \\ \leq & \left(\alpha f_1(\boldsymbol{x})+(1-\alpha) f_1(\boldsymbol{y})\right)+\left(\alpha f_2(\boldsymbol{x})+(1-\alpha) f_2(\boldsymbol{y})\right) \\ & \quad \text { by convexity of } f_1 \text { and } f_2 \\ = & \alpha\left(f_1(\boldsymbol{x})+f_2(\boldsymbol{x})\right)+(1-\alpha)\left(f_1(\boldsymbol{y})+f_2(\boldsymbol{y})\right) \\ = & \alpha f_3(\boldsymbol{x})+(1-\alpha) f_3(\boldsymbol{y}), \end{aligned}$$

which implies that $f_3$ is convex. This theorem implies that for any given collection of convex functions $f_1, \ldots, f_{\ell}$ and nonnegative numbers $c_1, \ldots, c_{\ell}$, the function $c_1 f_2+\cdots+c_{\ell} f_{\ell}$ is convex. It is similarly straightforward to show that the function $\max \left\{f_1, \ldots, f_{\ell}\right\}$ is convex. We now define the notion of strict convexity.

Definition

A function $f: \Omega \rightarrow \mathbb{R}$ on a convex set $\Omega \subset \mathbb{R}^n$ is strictly convex if for all $\boldsymbol{x}, \boldsymbol{y} \in \Omega, \boldsymbol{x} \neq \boldsymbol{y}$, and $\alpha \in(0,1)$, we have

$$f(\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y})<\alpha f(\boldsymbol{x})+(1-\alpha) f(\boldsymbol{y}) .$$

From this definition, we see that for a strictly convex function, all points on the open line segment connecting the points $\left[\boldsymbol{x}^{\top}, f(\boldsymbol{x})\right]^{\top}$ and $\left[\boldsymbol{y}^{\top}, f(\boldsymbol{y})\right]^{\top}$ lie (strictly) above the graph of $f$.

Definition

A function $f: \Omega \rightarrow \mathbb{R}$ on a convex set $\Omega \subset \mathbb{R}^n$ is (strictly) concave if $-f$ is (strictly) convex.

Convex optimization problems in standard form

A convex optimization problem is one of the form

$$\begin{array}{ll} \text { minimize } & f_0(x) \\ \text { subject to } & f_i(x) \leq 0, \quad i=1, \ldots, m \\ & a_i^T x=b_i, \quad i=1, \ldots, p, \end{array}$$

where $f_0, \ldots, f_m$ are convex functions. The convex problem has three additional requirements:

• the objective function must be convex,
• the inequality constraint functions must be convex,
• the equality constraint functions $h_i(x)=a_i^Tx-b_i$ must be affine.